Study Notes: Stanford CS336 Language Modeling from Scratch [5]
Building a Transformer Language Model: A Complete Guide
Ever wondered how ChatGPT and other language models actually work under the hood? Let’s build one from scratch and understand every component.This guide explains how to build a Transformer language model from scratch using PyTorch. We’ll cover each building block and show how they work together to create a complete language model.
Table of Contents
- Overview
- Basic Building Blocks
- Core Components
- Advanced Components
- Putting It All Together
- The Complete Transformer
Overview
A Transformer language model is essentially a sophisticated pattern recognition system that learns to predict the next word in a sequence. Think of it as an incredibly advanced autocomplete that understands context, grammar, and meaning. By the end of this guide, you’ll understand:
- How words become numbers a neural network can process
- How attention mechanisms let models “focus” on relevant information
- How all the pieces fit together to create a complete language model
Before diving into details, let’s understand the overall architecture:
Input: “The cat sat on the”
⬇️Step 1: Convert words to numbers (embeddings)
Step 2: Process through multiple transformer blocks:
- Attention: “What should I focus on?”
- Feed-forward: “What patterns do I see?”
Step 3: Predict next word probabilities
⬇️Output: “mat” (85%), “chair” (10%), “floor” (5%)
Now let’s build each component step by step.
Basic Building Blocks
1. Linear Layer (cs336_basics/linear.py)
What it does: A linear layer is the most basic building block of neural networks. It takes input numbers and transforms them using a mathematical operation: output = input × weight.
Why we need it: Linear layers let the model learn patterns by adjusting their weights during training.
# Example: Transform 64 dimensions to 128 dimensions
linear = Linear(in_features=64, out_features=128)
# If input is shape (batch_size, 64), output will be (batch_size, 128)
Implementation:
import math
import torch
import torch.nn as nn
class Linear(nn.Module):
"""
A linear transformation module that inherits from torch.nn.Module.
Performs y = xW^T without bias.
"""
def __init__(self, in_features: int, out_features: int, device=None, dtype=None):
super().__init__()
self.in_features = in_features
self.out_features = out_features
# Create weight parameter W (not W^T) for memory ordering reasons
self.W = nn.Parameter(torch.empty(out_features, in_features, device=device, dtype=dtype))
self.reset_parameters()
def reset_parameters(self):
"""
Initialize weights using truncated normal distribution.
Linear weights: N(μ=0, σ²=2/(d_in + d_out)) truncated at [-3σ, 3σ]
"""
std = math.sqrt(2.0 / (self.in_features + self.out_features))
with torch.no_grad():
torch.nn.init.trunc_normal_(self.W, mean=0.0, std=std, a=-3*std, b=3*std)
def forward(self, x: torch.Tensor) -> torch.Tensor:
"""Apply the linear transformation to the input."""
return torch.matmul(x, self.W.T)
Key features:
- No bias term (simpler than standard PyTorch Linear)
- Weights initialized using truncated normal distribution
- Used throughout the Transformer for projections and transformations
2. Embedding Layer (cs336_basics/embedding.py)
What it does: Converts discrete tokens (like word IDs) into dense vector representations that neural networks can work with.
Think of it like this: If words were people, embeddings would be detailed personality profiles. Similar words get similar profiles.
# Example: Convert word IDs to 512-dimensional vectors
embedding = Embedding(num_embeddings=10000, embedding_dim=512)
# Input: [5, 23, 156] (word IDs)
# Output: 3 vectors, each with 512 numbers
Implementation:
import torch
import torch.nn as nn
class Embedding(nn.Module):
"""
An embedding module that inherits from torch.nn.Module.
Performs embedding lookup by indexing into an embedding matrix.
"""
def __init__(self, num_embeddings: int, embedding_dim: int, device=None, dtype=None):
super().__init__()
self.num_embeddings = num_embeddings
self.embedding_dim = embedding_dim
# Create embedding matrix parameter with shape (vocab_size, d_model)
# Store with d_model as the final dimension
self.embeddings = nn.Parameter(torch.empty(num_embeddings, embedding_dim,
device=device, dtype=dtype))
self.reset_parameters()
def reset_parameters(self):
"""
Initialize embedding weights using truncated normal distribution.
Embedding: N(μ=0, σ²=1) truncated at [-3, 3]
"""
with torch.no_grad():
torch.nn.init.trunc_normal_(self.embeddings, mean=0.0, std=1.0, a=-3.0, b=3.0)
def forward(self, token_ids: torch.Tensor) -> torch.Tensor:
"""
Lookup the embedding vectors for the given token IDs.
Args:
token_ids: Token IDs with shape (batch_size, sequence_length)
Returns:
Embedding vectors with shape (batch_size, sequence_length, embedding_dim)
"""
return self.embeddings[token_ids]
Key features:
- Maps discrete tokens to continuous vectors
- Similar words learn to have similar embeddings
- The embedding matrix is learned during training
3. Softmax Function (cs336_basics/softmax.py)
What it does: Converts a list of numbers into probabilities that sum to 1.
Why we need it: At the end of the model, we need probabilities for each possible next word.
# Example: Convert logits to probabilities
logits = [2.0, 1.0, 0.1] # Raw scores
probabilities = softmax(logits) # [0.659, 0.242, 0.099] - sums to 1.0
Implementation:
import torch
def softmax(x: torch.Tensor, dim: int) -> torch.Tensor:
"""
Apply the softmax operation to a tensor along the specified dimension.
Uses the numerical stability trick of subtracting the maximum value
from all elements before applying exponential.
Args:
x: torch.Tensor - Input tensor
dim: int - Dimension along which to apply softmax
Returns:
torch.Tensor - Output tensor with same shape as input, with normalized
probability distribution along the specified dimension
"""
# Subtract maximum for numerical stability
# keepdim=True ensures the shape is preserved for broadcasting
max_vals = torch.max(x, dim=dim, keepdim=True)[0]
x_stable = x - max_vals
# Apply exponential
exp_vals = torch.exp(x_stable)
# Compute sum along the specified dimension
sum_exp = torch.sum(exp_vals, dim=dim, keepdim=True)
# Normalize to get probabilities
return exp_vals / sum_exp
Key features:
- Uses numerical stability trick (subtracts max value)
- Higher input values become higher probabilities
- All outputs sum to exactly 1.0
Core Components
4. RMSNorm (cs336_basics/rmsnorm.py)
What it does: Normalizes the inputs to keep the model stable during training. It’s like adjusting the volume on different audio channels to keep them balanced.
Formula: RMSNorm(x) = x / RMS(x) * learnable_scale
# Example: Normalize 512-dimensional vectors
rmsnorm = RMSNorm(d_model=512)
# Keeps all dimensions on a similar scale
Implementation:
import torch
import torch.nn as nn
class RMSNorm(nn.Module):
"""
RMSNorm (Root Mean Square Layer Normalization) module.
Rescales each activation a_i as: RMSNorm(a_i) = a_i/RMS(a) * g_i
where RMS(a) = sqrt(1/d_model * ∑a^2_i + ε)
"""
def __init__(self, d_model: int, eps: float = 1e-5, device=None, dtype=None):
super().__init__()
self.d_model = d_model
self.eps = eps
# Learnable gain parameter g_i
self.g = nn.Parameter(torch.ones(d_model, device=device, dtype=dtype))
def forward(self, x: torch.Tensor) -> torch.Tensor:
# Store original dtype
in_dtype = x.dtype
x = x.to(torch.float32)
# Compute RMS: sqrt(1/d_model * ∑a^2_i + ε)
# Mean of squares over the last dimension (d_model)
mean_square = torch.mean(x ** 2, dim=-1, keepdim=True)
rms = torch.sqrt(mean_square + self.eps)
# Apply RMSNorm: a_i/RMS(a) * g_i
result = (x / rms) * self.g
# Return in original dtype
return result.to(in_dtype)
Why it’s important:
- Prevents values from becoming too large or too small
- Helps the model train faster and more stably
- Applied before major operations in the Transformer
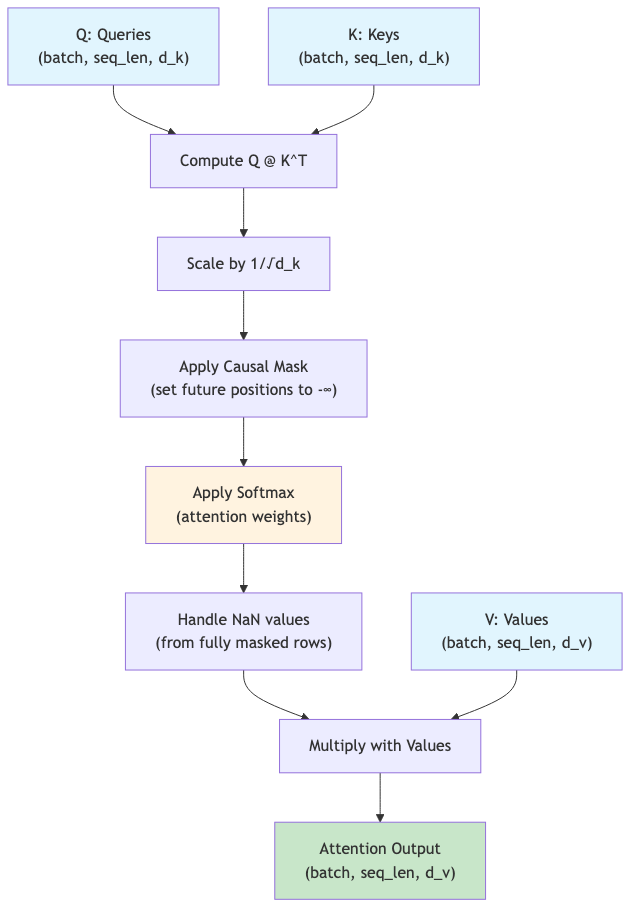
5. Attention Mechanism (cs336_basics/attention.py)
What it does: Allows the model to focus on different parts of the input when making predictions. Like highlighting important words when reading.
Key concepts:
- Queries (Q): “What am I looking for?”
- Keys (K): “What information is available?”
- Values (V): “What is the actual information?”
- Dimension Requirements
# Q: [batch, seq_len_q, d_k] - Query dimension # K: [batch, seq_len_k, d_k] - Key dimension # V: [batch, seq_len_v, d_v] - Value dimension # Requirements: # 1. Q and K MUST have same d_k (for dot product) # 2. K and V MUST have same seq_len (they describe the same items) # 3. V can have different d_v (output dimension can differ)
# Attention formula: Attention(Q,K,V) = softmax(Q×K^T / √d_k) × V
attention_output = scaled_dot_product_attention(Q, K, V, mask)
Implementation:
import torch
import math
from .softmax import softmax
def scaled_dot_product_attention(Q: torch.Tensor, K: torch.Tensor, V: torch.Tensor, mask: torch.Tensor = None) -> torch.Tensor:
"""
Scaled dot-product attention implementation.
Computes: Attention(Q, K, V) = softmax(Q @ K^T / sqrt(d_k)) @ V
"""
# Get dimensions
d_k = Q.shape[-1]
# Compute scaled dot-product: Q @ K^T / sqrt(d_k)
scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(d_k)
# Apply mask if provided
if mask is not None:
# Where mask is False, set scores to negative infinity
# This will make softmax output 0 for those positions
scores = scores.masked_fill(~mask, float('-inf'))
# Apply softmax along the last dimension (over keys)
attention_weights = softmax(scores, dim=-1)
# Handle the case where entire rows are masked (all -inf)
if mask is not None:
# If a row is entirely masked, attention_weights will have NaN
# Replace NaN with 0
attention_weights = torch.where(torch.isnan(attention_weights),
torch.zeros_like(attention_weights),
attention_weights)
# Apply attention to values
output = torch.matmul(attention_weights, V)
return output
Attention Mechanism Flow:
Features:
- Causal masking: Prevents looking at future words (essential for language modeling)
- Scaling: Divides by √d_k for numerical stability
- Flexible dimensions: Works with any number of batch dimensions
6. Rotary Position Embedding (RoPE) (cs336_basics/rope.py)
What it does: Tells the model where each word is positioned in the sequence by rotating the attention vectors based on position.
Why it’s needed: Without position information, “cat sat on mat” and “mat sat on cat” would look identical to the model.
# RoPE rotates query and key vectors based on their position
rope = RotaryPositionalEmbedding(theta=10000.0, d_k=64, max_seq_len=512)
rotated_queries = rope(queries, token_positions)
Implementation:
import torch
import torch.nn as nn
class RotaryPositionalEmbedding(nn.Module):
"""
Rotary Positional Embedding (RoPE) module.
Applies rotary positional embeddings to input tensors by rotating pairs of dimensions
based on their position in the sequence.
"""
def __init__(self, theta: float, d_k: int, max_seq_len: int, device=None):
super().__init__()
self.theta = theta
self.d_k = d_k
self.max_seq_len = max_seq_len
# Precompute the frequency values for each dimension pair
assert d_k % 2 == 0, "d_k must be even for RoPE"
# Create frequency values: theta^(-2i/d_k) for i = 0, 1, ..., d_k/2 - 1
dim_indices = torch.arange(0, d_k // 2, dtype=torch.float32, device=device)
freqs = theta ** (-2.0 * dim_indices / d_k)
# Create position indices for the maximum sequence length
positions = torch.arange(max_seq_len, dtype=torch.float32, device=device)
# Compute the angles: position * frequency for each position and frequency
angles = torch.outer(positions, freqs)
# Precompute cos and sin values
# We need to repeat each value twice to match the pairing structure
cos_vals = torch.repeat_interleave(torch.cos(angles), 2, dim=-1)
sin_vals = torch.repeat_interleave(torch.sin(angles), 2, dim=-1)
# Register as buffers so they move with the module
self.register_buffer('cos_cached', cos_vals)
self.register_buffer('sin_cached', sin_vals)
def _rotate_half(self, x):
"""
Rotate the last dimension of x by swapping and negating pairs of elements.
For RoPE, we rotate pairs of dimensions: (x1, x2) -> (-x2, x1)
"""
# Split into two halves and swap with negation
x1 = x[..., ::2] # Even indices (0, 2, 4, ...)
x2 = x[..., 1::2] # Odd indices (1, 3, 5, ...)
# Interleave -x2 and x1
rotated = torch.stack((-x2, x1), dim=-1)
return rotated.flatten(start_dim=-2)
def forward(self, x: torch.Tensor, token_positions: torch.Tensor) -> torch.Tensor:
# Extract cos and sin values for the given positions
cos_vals = self.cos_cached[token_positions] # (..., seq_len, d_k)
sin_vals = self.sin_cached[token_positions] # (..., seq_len, d_k)
# Apply RoPE: x * cos + rotate_half(x) * sin
rotated_x = self._rotate_half(x)
return x * cos_vals + rotated_x * sin_vals
Key features:
- Encodes position directly into attention mechanism
- Works well with different sequence lengths
- Applied to queries and keys, but not values, because positional information is used for attention computation, not for the content being retrieved
Advanced Components
7. SwiGLU Feed-Forward Network (cs336_basics/swiglu.py)
What it does: A sophisticated feed-forward network that processes information after attention. It’s like a specialized filter that enhances certain patterns.
Components:
- SiLU activation:
SiLU(x) = x × sigmoid(x)- smoother than ReLU - Gated Linear Unit: Combines two transformations with element-wise multiplication
- Three linear layers: W1, W2, W3
# SwiGLU formula: W2(SiLU(W1×x) ⊙ W3×x)
# ⊙ means element-wise multiplication
swiglu = SwiGLU(d_model=512, d_ff=1365) # d_ff ≈ 8/3 × d_model
Implementation:
import torch
import torch.nn as nn
from .linear import Linear
def silu(x: torch.Tensor) -> torch.Tensor:
"""
SiLU (Swish) activation function: SiLU(x) = x * sigmoid(x) = x / (1 + e^(-x))
"""
return x * torch.sigmoid(x)
class SwiGLU(nn.Module):
"""
SwiGLU: SiLU-based Gated Linear Unit
FFN(x) = SwiGLU(x, W1, W2, W3) = W2(SiLU(W1x) ⊙ W3x)
where ⊙ represents element-wise multiplication
"""
def __init__(self, d_model: int, d_ff: int = None, device=None, dtype=None):
super().__init__()
self.d_model = d_model
# Calculate d_ff if not provided: 8/3 * d_model, rounded to nearest multiple of 64
if d_ff is None:
d_ff = int(8/3 * d_model)
# Round to nearest multiple of 64
d_ff = ((d_ff + 31) // 64) * 64
self.d_ff = d_ff
# Three linear transformations: W1, W2, W3
self.W1 = Linear(d_model, d_ff, device=device, dtype=dtype)
self.W2 = Linear(d_ff, d_model, device=device, dtype=dtype)
self.W3 = Linear(d_model, d_ff, device=device, dtype=dtype)
def forward(self, x: torch.Tensor) -> torch.Tensor:
# SwiGLU(x, W1, W2, W3) = W2(SiLU(W1x) ⊙ W3x)
w1_output = self.W1(x) # (..., d_ff)
w3_output = self.W3(x) # (..., d_ff)
# Apply SiLU to W1 output and element-wise multiply with W3 output
gated = silu(w1_output) * w3_output # (..., d_ff)
# Final linear transformation
return self.W2(gated) # (..., d_model)
SwiGLU Architecture:
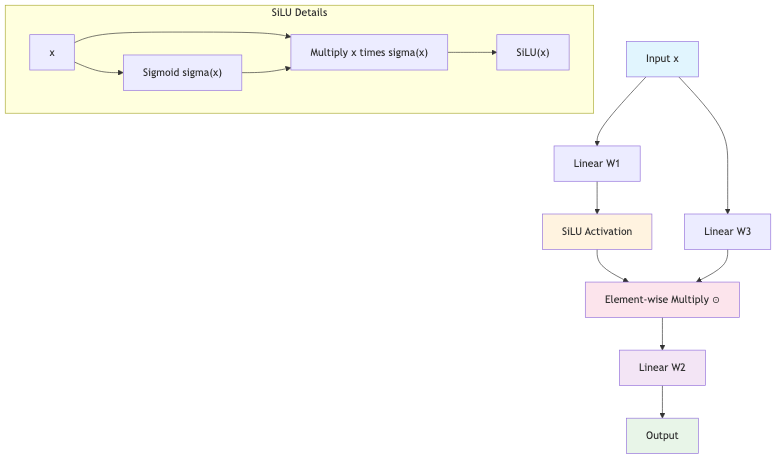
Why SwiGLU:
- More expressive than simple feed-forward networks
- Gating mechanism helps control information flow
- Proven to work better in practice for language models
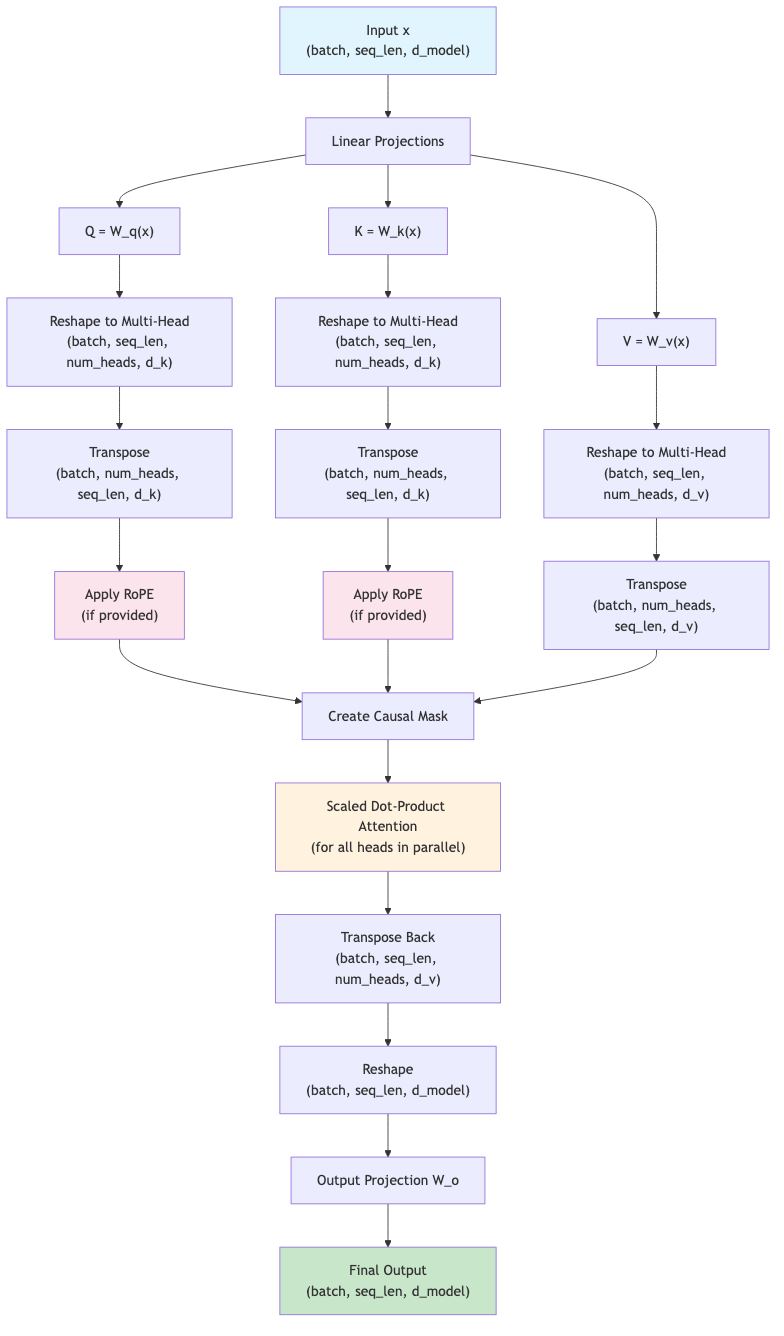
8. Multi-Head Self-Attention (cs336_basics/multihead_attention.py)
What it does: Implements the complete multi-head attention mechanism with causal masking and RoPE support. This is where the model learns to focus on relevant parts of the input sequence.
Key features:
- Multiple attention heads: Each head can focus on different types of relationships
- Causal masking: Prevents looking at future tokens
- RoPE integration: Position encoding directly in the attention mechanism
- Parallel computation: All heads computed simultaneously
Why Multiple Heads?
The motivation is representation power and diversity of attention patterns.
- Different subspaces of information
- Each head learns its own set of projection matrices (
W_q,W_k,W_v). - Each head looks at the input through a different lens, projecting embeddings into different subspaces.
- One head might focus on syntactic relations, another on semantics, another on positional information.
- Each head learns its own set of projection matrices (
- Richer attention patterns
- Multiple heads can attend to different tokens simultaneously.
- Example: in translation, one head might track word order, another align nouns, another focus on verbs.
- Stability and expressiveness
- A single attention head is essentially a weighted average — too simple.
- Multiple heads prevent the model from collapsing into one dominant pattern and encourage diverse contextualization.
How to Select the Number of Heads?
There’s no universal formula, but here are practical guidelines:
- Divisibility with model dimension
- Embedding dimension
d_modelmust be divisible by the number of headsh. - Each head gets a sub-dimension
d_k = d_model / h. - Example:
d_model = 512, common choices areh = 8(d_k = 64) orh = 16(d_k = 32).
- Embedding dimension
- Balance between capacity and efficiency
- Too few heads → each head has a large
d_k→ less diversity, harder to capture multiple relations. - Too many heads → each head has a tiny
d_k→ may lose expressive power, and overhead grows.
- Too few heads → each head has a large
- Empirical rules from practice
- Original Transformer (Vaswani et al.):
d_model = 512,h = 8→d_k = 64.
- BERT-base:
d_model = 768,h = 12→d_k = 64.
- BERT-large / GPT-3 style models:
d_model = 1024–12288,h = 16–96, often keepingd_k ≈ 64.
- In practice, many architectures fix
d_k ≈ 64per head and scalehwith model size.
- Original Transformer (Vaswani et al.):
- Scaling law intuition
- Larger models tend to use more heads.
- But going below
d_k < 32per head often hurts performance — each head needs enough dimensions to be useful.
Intuition
- One head = one spotlight. It can only focus on one kind of relationship at a time.
- Multiple heads = multiple spotlights. Each head looks at different aspects, and their outputs are concatenated and mixed to form a richer representation.
Implementation:
import torch
import torch.nn as nn
from .linear import Linear
from .attention import scaled_dot_product_attention
from .rope import RotaryPositionalEmbedding
class MultiHeadSelfAttention(nn.Module):
"""
Causal Multi-Head Self-Attention module.
Implements the multi-head self-attention mechanism with causal masking
to prevent attending to future tokens.
"""
def __init__(self, d_model: int, num_heads: int, device=None, dtype=None):
super().__init__()
self.d_model = d_model
self.num_heads = num_heads
# Following Vaswani et al., d_k = d_v = d_model / num_heads
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
self.d_k = d_model // num_heads
self.d_v = d_model // num_heads
# Linear projections for Q, K, V
self.W_q = Linear(d_model, d_model, device=device, dtype=dtype)
self.W_k = Linear(d_model, d_model, device=device, dtype=dtype)
self.W_v = Linear(d_model, d_model, device=device, dtype=dtype)
# Output projection
self.W_o = Linear(d_model, d_model, device=device, dtype=dtype)
def forward(self, x: torch.Tensor, rope: RotaryPositionalEmbedding = None, token_positions: torch.Tensor = None) -> torch.Tensor:
batch_size, seq_len, d_model = x.shape
# Apply linear projections
Q = self.W_q(x) # (batch_size, seq_len, d_model)
K = self.W_k(x) # (batch_size, seq_len, d_model)
V = self.W_v(x) # (batch_size, seq_len, d_model)
# Reshape to multi-head format
Q = Q.view(batch_size, seq_len, self.num_heads, self.d_k)
K = K.view(batch_size, seq_len, self.num_heads, self.d_k)
V = V.view(batch_size, seq_len, self.num_heads, self.d_v)
# Transpose to (batch_size, num_heads, seq_len, d_k/d_v)
Q = Q.transpose(1, 2)
K = K.transpose(1, 2)
V = V.transpose(1, 2)
# Apply RoPE if provided (only to Q and K, not V)
if rope is not None and token_positions is not None:
# Reshape for RoPE
Q_rope = Q.contiguous().view(batch_size * self.num_heads, seq_len, self.d_k)
K_rope = K.contiguous().view(batch_size * self.num_heads, seq_len, self.d_k)
# Expand token_positions to match
token_positions_expanded = token_positions.unsqueeze(1).expand(batch_size, self.num_heads, seq_len).contiguous().view(batch_size * self.num_heads, seq_len)
# Apply RoPE
Q_rope = rope(Q_rope, token_positions_expanded)
K_rope = rope(K_rope, token_positions_expanded)
# Reshape back
Q = Q_rope.view(batch_size, self.num_heads, seq_len, self.d_k)
K = K_rope.view(batch_size, self.num_heads, seq_len, self.d_k)
# Create causal mask: lower triangular matrix
causal_mask = torch.triu(torch.ones(seq_len, seq_len, dtype=torch.bool, device=x.device), diagonal=1)
causal_mask = ~causal_mask # Invert: True means attend, False means don't attend
# Apply scaled dot-product attention
attn_output = scaled_dot_product_attention(Q, K, V, causal_mask)
# Transpose back and reshape
attn_output = attn_output.transpose(1, 2)
attn_output = attn_output.contiguous().view(batch_size, seq_len, d_model)
# Apply output projection
output = self.W_o(attn_output)
return output
Multi-Head Attention Flow:
Putting It All Together
9. Transformer Block (cs336_basics/transformer_block.py)
What it does: Combines attention and feed-forward processing with residual connections and normalization. This is the core building block of the Transformer.
Architecture (Pre-Norm):
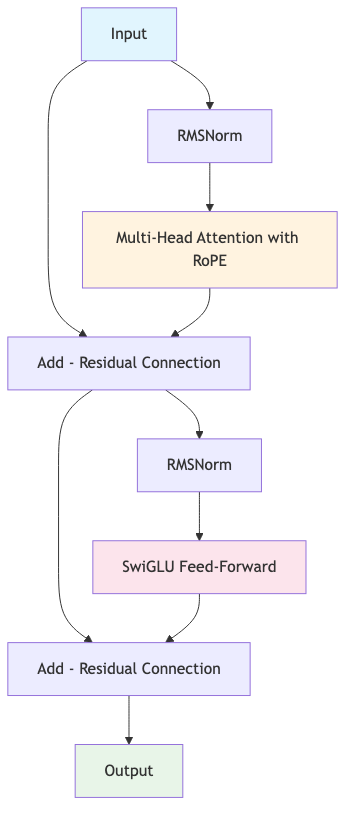
# Each transformer block does:
# 1. x = x + attention(norm(x))
# 2. x = x + feedforward(norm(x))
transformer_block = TransformerBlock(d_model=512, num_heads=8, d_ff=1365)
Key concepts:
- Residual connections: Add input to output (
x + f(x)) - helps training deep networks - Pre-normalization: Apply normalization before operations, not after
- Multi-head attention: Run multiple attention operations in parallel
Implementation:
import torch
import torch.nn as nn
from .rmsnorm import RMSNorm
from .multihead_attention import MultiHeadSelfAttention
from .swiglu import SwiGLU
from .rope import RotaryPositionalEmbedding
class TransformerBlock(nn.Module):
"""
A pre-norm Transformer block as shown in Figure 2.
Architecture (from bottom to top):
1. Input tensor
2. Norm -> Causal Multi-Head Self-Attention w/ RoPE -> Add (residual)
3. Norm -> Position-Wise Feed-Forward -> Add (residual)
4. Output tensor
"""
def __init__(self, d_model: int, num_heads: int, d_ff: int, device=None, dtype=None):
super().__init__()
self.d_model = d_model
self.num_heads = num_heads
self.d_ff = d_ff
# Layer normalization for the two sublayers (RMSNorm)
self.ln1 = RMSNorm(d_model, device=device, dtype=dtype) # Before attention
self.ln2 = RMSNorm(d_model, device=device, dtype=dtype) # Before feed-forward
# Causal Multi-Head Self-Attention w/ RoPE
self.attn = MultiHeadSelfAttention(d_model, num_heads, device=device, dtype=dtype)
# Position-Wise Feed-Forward (using SwiGLU)
self.ffn = SwiGLU(d_model, d_ff, device=device, dtype=dtype)
def forward(self, x: torch.Tensor, rope: RotaryPositionalEmbedding = None, token_positions: torch.Tensor = None) -> torch.Tensor:
# First sublayer: Norm -> Causal Multi-Head Self-Attention w/ RoPE -> Add
norm1_output = self.ln1(x)
attn_output = self.attn(norm1_output, rope=rope, token_positions=token_positions)
x = x + attn_output # Residual connection
# Second sublayer: Norm -> Position-Wise Feed-Forward -> Add
norm2_output = self.ln2(x)
ffn_output = self.ffn(norm2_output)
x = x + ffn_output # Residual connection
return x
The Complete Transformer
10. Transformer Language Model (cs336_basics/transformer_lm.py)
What it does: Combines everything into a complete language model that can predict the next word in a sequence.
Full Architecture:
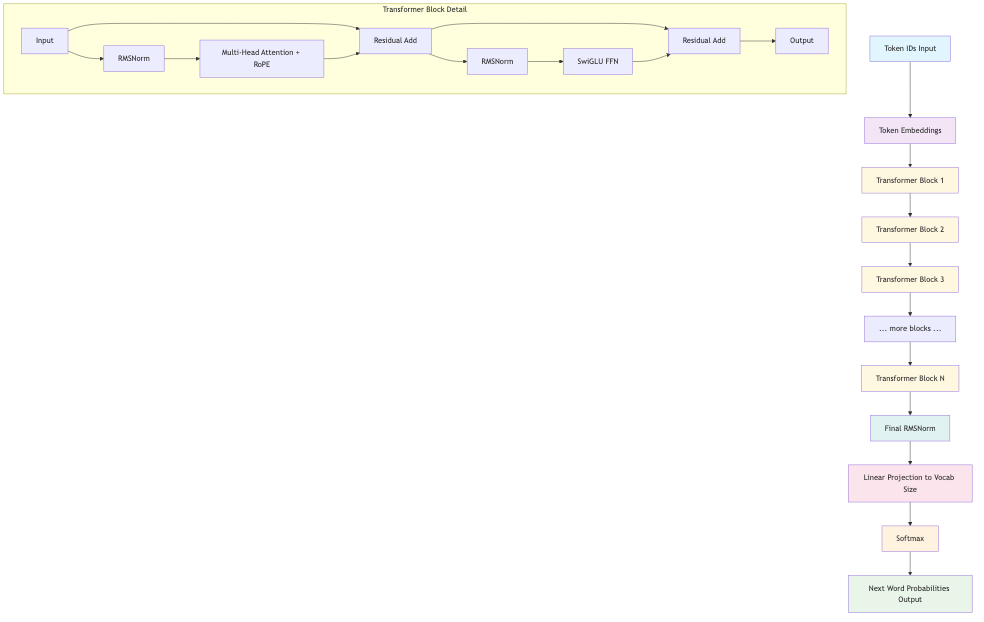
Architecture Flow:
- Token IDs → Input integers representing words/subwords
- Token Embeddings → Convert IDs to dense vectors
- Transformer Blocks (repeated num_layers times):
- RMSNorm → Multi-Head Attention (with RoPE) → Residual connection
- RMSNorm → SwiGLU Feed-Forward → Residual connection
- Final RMSNorm → Normalize before output
- Linear Head → Project to vocabulary size
- Softmax → Convert to probabilities (optional)
How it works:
- Input Processing: Convert word IDs to embeddings
- Pattern Recognition: Each Transformer block learns different patterns
- Output Generation: Final layer predicts next word probabilities
# Complete model
model = TransformerLM(
vocab_size=10000, # Number of possible words
context_length=512, # Maximum sequence length
d_model=512, # Model dimension
num_layers=6, # Number of transformer blocks
num_heads=8, # Number of attention heads
d_ff=1365 # Feed-forward dimension
)
# Usage
logits = model(input_ids) # Get next-word predictions
Complete Implementation:
import torch
import torch.nn as nn
from .embedding import Embedding
from .transformer_block import TransformerBlock
from .rmsnorm import RMSNorm
from .linear import Linear
from .rope import RotaryPositionalEmbedding
from .softmax import softmax
class TransformerLM(nn.Module):
"""
A Transformer language model as described in Figure 1.
Architecture (from bottom to top):
1. Inputs (token IDs)
2. Token Embedding
3. Multiple Transformer Blocks (num_layers)
4. Norm (RMSNorm)
5. Linear (Output Embedding)
6. Softmax
7. Output Probabilities
"""
def __init__(
self,
vocab_size: int,
context_length: int,
d_model: int,
num_layers: int,
num_heads: int,
d_ff: int,
rope_theta: float = 10000.0,
device=None,
dtype=None
):
super().__init__()
self.vocab_size = vocab_size
self.context_length = context_length
self.d_model = d_model
self.num_layers = num_layers
self.num_heads = num_heads
self.d_ff = d_ff
self.rope_theta = rope_theta
# Token Embedding
self.token_embeddings = Embedding(vocab_size, d_model, device=device, dtype=dtype)
# Transformer Blocks
self.layers = nn.ModuleList([
TransformerBlock(d_model, num_heads, d_ff, device=device, dtype=dtype)
for _ in range(num_layers)
])
# Final layer norm
self.ln_f = RMSNorm(d_model, device=device, dtype=dtype)
# Output projection (Linear - Output Embedding)
self.lm_head = Linear(d_model, vocab_size, device=device, dtype=dtype)
# RoPE module
d_k = d_model // num_heads
self.rope = RotaryPositionalEmbedding(
theta=rope_theta,
d_k=d_k,
max_seq_len=context_length,
device=device
)
def forward(self, input_ids: torch.Tensor, apply_softmax: bool = True) -> torch.Tensor:
batch_size, seq_len = input_ids.shape
# Generate token positions for RoPE
token_positions = torch.arange(seq_len, device=input_ids.device).unsqueeze(0).expand(batch_size, -1)
# Token Embedding
x = self.token_embeddings(input_ids) # (batch_size, seq_len, d_model)
# Apply Transformer blocks
for layer in self.layers:
x = layer(x, rope=self.rope, token_positions=token_positions)
# Final layer norm
x = self.ln_f(x) # (batch_size, seq_len, d_model)
# Output projection
logits = self.lm_head(x) # (batch_size, seq_len, vocab_size)
# Apply softmax if requested
if apply_softmax:
# Apply softmax over the vocabulary dimension (last dimension)
output_probs = softmax(logits, dim=-1)
return output_probs
else:
return logits
How Everything Works Together
- Token Embeddings convert words to vectors the model can process
- RMSNorm keeps values stable before major operations
- Attention lets the model look at relevant previous words
- RoPE tells attention where each word is positioned
- SwiGLU processes information after attention
- Linear layers transform dimensions throughout the model
- Softmax converts final outputs to word probabilities
- Transformer blocks stack these operations to learn complex patterns
The beauty of this architecture is its simplicity and effectiveness. With these building blocks, we can now understand the core technology behind ChatGPT, GPT-4, and other large language models.